Introduction: Cells exert traction forces on the extracellular matrix through focal adhesions in order to propel themselves. It is accessible to measure the cellular traction force by using three-dimensional traction force microscopy and finite element method[1]-[4]. However, the method is limited by the beads density and the difficulty of tracking beads in whole substrate. With recent technological advancements, beads can be concentrated on the top of the polyacrylamide (PA) substrates as surface beads. In that case, it will be easier to track the displacement and get more information by using higher beads density. Therefore, it is important to understand the effect of surface concentrated beads distribution considering all the x, y, and z components of the displacements.
Materials and Methods: We created two different conditions, BC1 and BC2, as shown in Fig. 1 to simulate the out-of-plane traction forces and to optimize the process. Then, we compared two conditions by computing the traction field generated by cultured embryo fibroblast (REF) cells.
For simulation, a block model subjected to a ring-like shear and normal tractions was built by a finite element package ANSYS (12.1) to simulate the deformation, stress fields of the PA gel. For experiment, laser scanning confocal microscopy was used to take images of two states of the substrates. One was deformed due to cell traction forces and the other was the undeformed state. The motion was measured from the micro-fluorescent beads embedded in the substrates, between two images. The cellular traction force was calculated from the x, y, and z displacements obtained from particle tracking.
Results and Discussion: For the case of single random simulation as shown in Fig. 2, the recovered traction pattern using BC1 better resembled the applied traction, though the magnitude was underestimated. In contrast, BC2 was more susceptible to error due to interpolation, and produced inaccurate peaks and distortion. It is effective for BC2 to eliminated inaccurate peaks by averaging 50 bootstrap samples. However, in contrast to BC2, BC1 is still closer to the simulated normal traction.
Fig.3 shows a REF cell on the substrate and the out-of-plane traction force of the two different analyses. It is evident that the experimental result shows the same trend as the single random distribution case. We find in our experiments that the presence of extreme peak with BC2 may be unfaithful, which is consistent with the single random case with BC2.
Conclusions: In general, the average inter-bead distance and the resolution of traction force are in inverse proportion. It is difficult to shorten the average inter-bead distance for whole-field beads due to tracking problem. However, we can track surface beads easily so it is accessible to shorten the average bead distance for BC1. In this study we find that BC1 is more accurate than the BC2 and is closer to the applied traction field. In the future, we will increase the beads density to get more information about displacement field to achieve higher resolution by using surface concentrated beads.
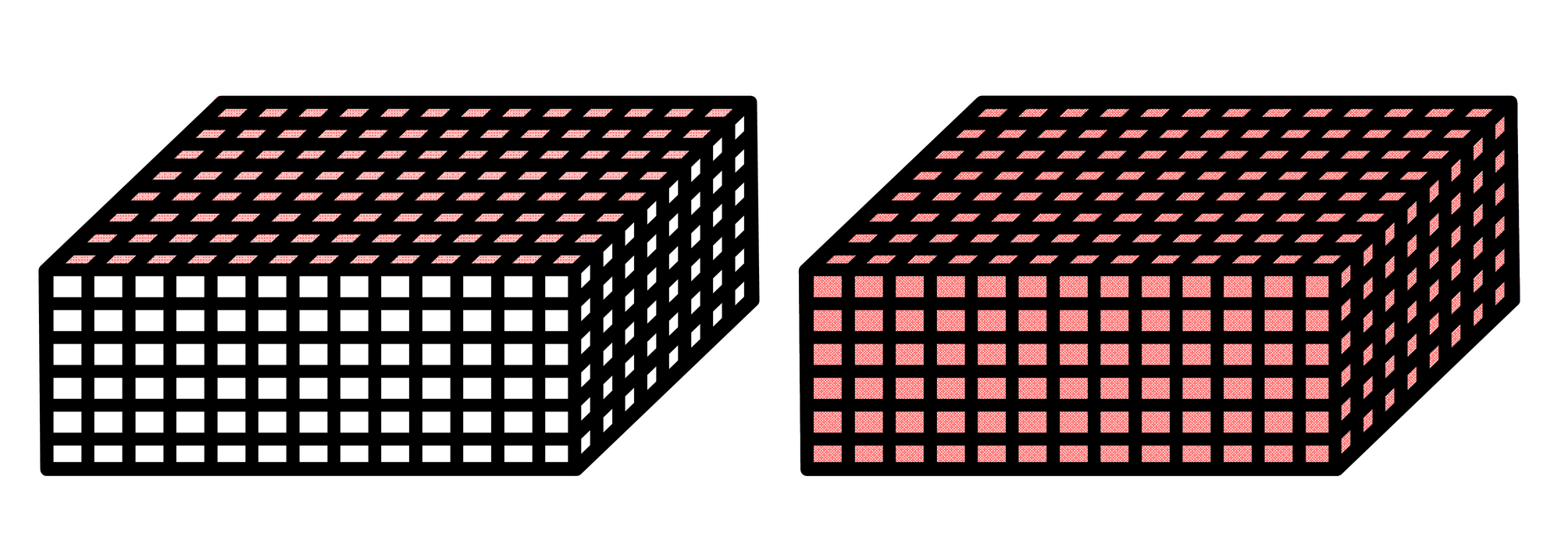
Fig. 1 The boundary condition of two situations: (a) BC1: The displacement field are prescribed at the nodes on top's surface. (b) BC2: The displacement field are prescribed at all the nodes in whole-field. (Red region is displacement field.)

Fig. 2 (a) BC1 (the upper left) (b) BC2 (the upper right) : Normal traction field with random displacement. (c) BC1 (the lower left) : (d) BC2 (the lower right) : Normal traction field with random displacement after 50 bootstrap iterations
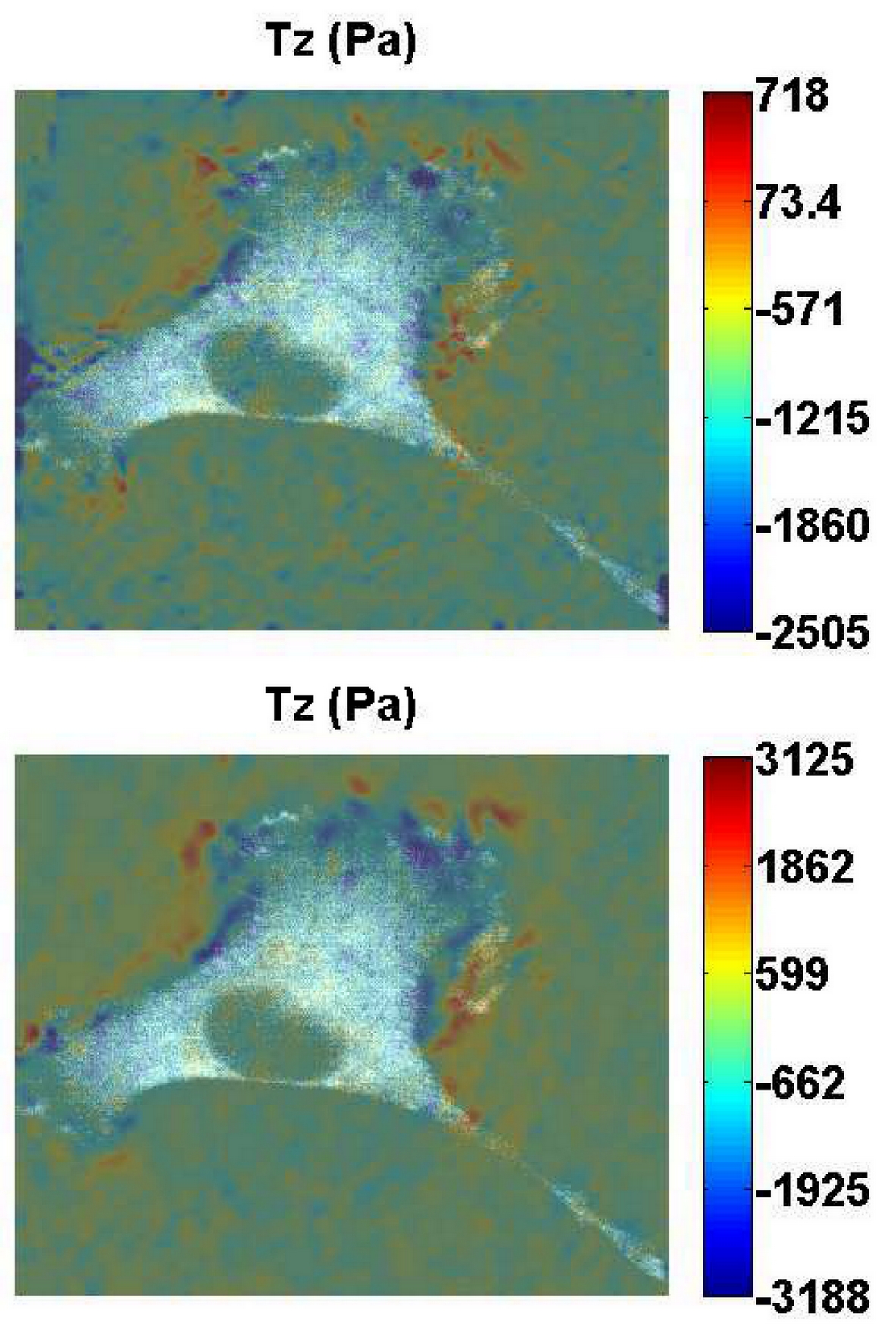
Fig. 3 (a) BC1 (b) BC2: The cell normal traction field analyzed by two situations
References:
[1] X. Tang, A. Tofangchi, S. V. Anand, and T. A. Saif, “A Novel Cell Traction Force Microscopy to Study Multi-Cellular System,” PLoS Comput. Biol., vol. 10, no. 6, 2014.
[2] B. Sabass, M. L. Gardel, C. M. Waterman, and U. S. Schwarz, “High resolution traction force microscopy based on experimental and computational advances.,” Biophys. J., vol. 94, no. 1, pp. 207–20, Jan. 2008.
[3] W. R. Legant, J. S. Miller, B. L. Blakely, D. M. Cohen, G. M. Genin, and C. S. Chen, “Measurement of mechanical tractions exerted by cells in three-dimensional matrices.,” Nat. Methods, vol. 7, no. 12, pp. 969–71, Dec. 2010.
[4] W. R. Legant, C. K. Choi, J. S. Miller, L. Shao, L. Gao, E. Betzig, and C. S. Chen, “Multidimensional traction force microscopy reveals out-of-plane rotational moments about focal adhesions.,” in Proceedings of the National Academy of Sciences of the United States of America, vol. 110, no. 3, 2013, pp. 881–6.